Prim’s Algorithm — Minimum Spanning Tree (MST)

In this post, we will explore Prim’s Algorithm, a greedy approach used to find the Minimum Spanning Tree (MST) of a weighted, undirected graph. We’ll also implement the algorithm in Go and walk through a visual example to solidify your understanding.

---

When Can We Use Prim’s Algorithm?

Prim’s Algorithm can be applied only when the graph satisfies the following conditions:

• The graph is undirected
• All edge weights are non-negative
• The graph is connected (there's a path between every pair of nodes)

❗ If the graph is disconnected, Prim’s algorithm will not generate a spanning tree that includes all vertices.

---

What Does It Do?

Prim’s Algorithm helps us find the Minimum Spanning Tree (MST) — a subset of the edges that:

• Connects all vertices in the graph
• Has no cycles
• Has the minimum total edge weight possible

---

Where Is It Used in Real Life?

Prim’s Algorithm is widely used in various domains:

• Designing road and highway networks (connecting cities with minimal cost)
• Laying out cables or pipelines (least amount of wire or pipe needed to connect buildings)
• Network design (connecting routers/switches efficiently)
• Cluster analysis in machine learning
• Utility planning (electricity, water supply, etc.)

---

Example (With Visualization)

Here’s a visual explanation of Prim’s Algorithm:

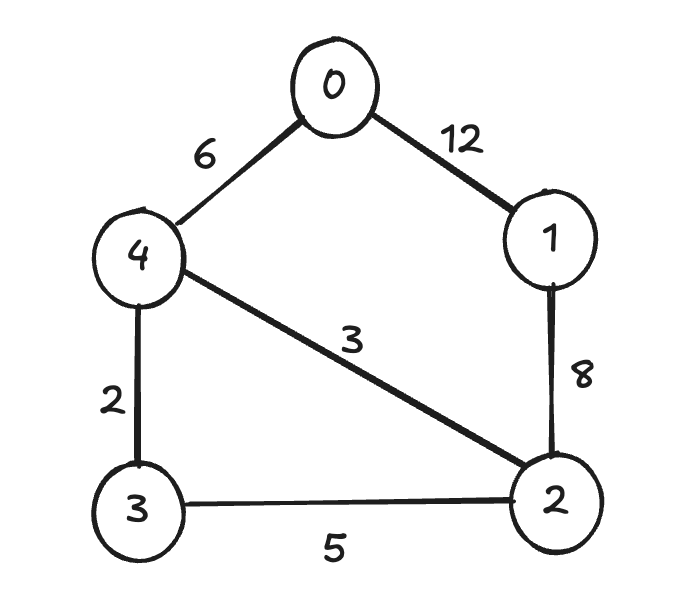
We start with Node 0 and build the Minimum Spanning Tree (MST) by always picking the lowest-weight edge that connects a visited node to an unvisited one.

Steps:

• Start at Node 0 Lowest edge: 0 → 4 (6) → Add to MST

• From 4 Lowest edge: 4 → 3 (2) → Add to MST

• From 3 Lowest edge: 4 → 2 (3) → Add to MST

• From 2 Lowest edge: 2 → 1 (8) → Add to MST

All nodes are now connected with the minimum total weight.

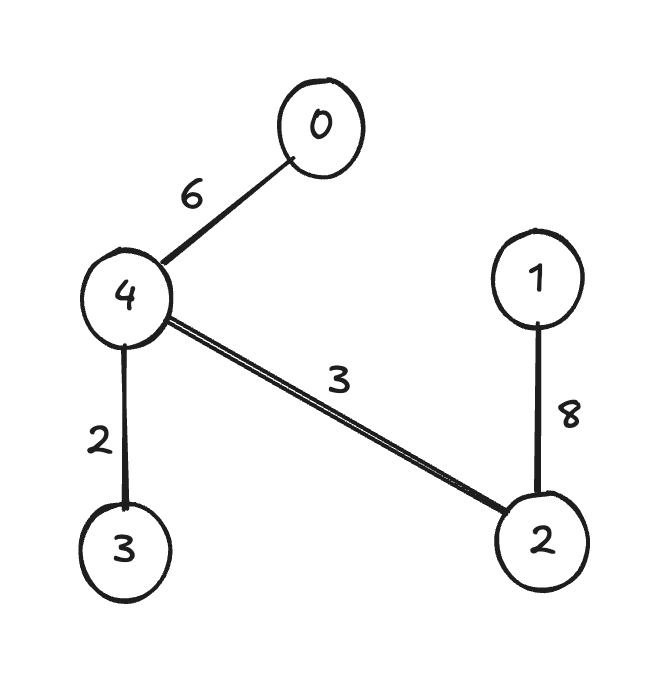
The edges in teal form the Minimum Spanning Tree.

---

🛠️ Go Implementation

package main

import (
    "container/heap"
    "fmt"
)

type MinHeap [][]int

func (h MinHeap) Len() int           { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i][2] < h[j][2] }
func (h MinHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(value any)    { *h = append(*h, value.([]int)) }
func (h *MinHeap) Pop() any {
    l := len(*h)
    val := (*h)[l-1]
    *h = (*h)[:l-1]
    return val
}

func printMst(edges [][][]int) [][][]int {
    mst := make([][][]int, len(edges))
    h := &MinHeap{}
    heap.Init(h)

    for _, edge := range edges[0] {
        heap.Push(h, []int{0, edge[0], edge[1]}) // from, to, weight
    }

    visited := map[int]bool{0: true}

    for h.Len() > 0 {
        edge := heap.Pop(h).([]int)
        from, to, weight := edge[0], edge[1], edge[2]

        if visited[to] {
            continue
        }

        visited[to] = true
        mst[from] = append(mst[from], []int{to, weight})
        mst[to] = append(mst[to], []int{from, weight})

        for _, next := range edges[to] {
            if !visited[next[0]] {
                heap.Push(h, []int{to, next[0], next[1]})
            }
        }
    }

    return mst
}

---

Sample Input

func main() {
    edges := [][][]int{
        {{1, 12}, {4, 6}},        // Node 0
        {{0, 12}, {2, 8}},        // Node 1
        {{1, 8}, {3, 5}, {4, 3}}, // Node 2
        {{2, 5}, {4, 2}},         // Node 3
        {{0, 6}, {2, 3}, {3, 2}}, // Node 4
    }

    mst := printMst(edges)
    fmt.Println("Minimum Spanning Tree:")
    for i, connections := range mst {
        for _, conn := range connections {
            fmt.Printf("%d -- %d (weight %d)\n", i, conn[0], conn[1])
        }
    }
}

---

Output

Minimum Spanning Tree:
0 -- 4 (weight 6)
1 -- 2 (weight 8)
2 -- 4 (weight 3)
2 -- 1 (weight 8)
3 -- 4 (weight 2)
4 -- 0 (weight 6)
4 -- 3 (weight 2)
4 -- 2 (weight 3)

---

⏱️ Time & Space Complexity

• Time Complexity: O(E log E) due to min-heap operations
• Space Complexity: O(V + E) for the heap and adjacency list

---

👍 Advantages

• Efficient for dense graphs
• Easy to implement with a min-heap
• Builds MST without sorting all edges

---

👎 Disadvantages

• Doesn’t work on directed graphs
• Fails on graphs with negative weights
• Requires the graph to be connected

---

Conclusion

Prim’s Algorithm is a powerful tool for finding MSTs in undirected graphs. It’s highly practical for infrastructure design, network planning, and clustering algorithms.

🧠 Remember: Use Prim’s when the graph is undirected, connected, and all weights are non-negative.

---

Feel free to follow my work on GitHub: Prim's Algorithm in Go.